Unraveling the Mysteries of Wave Propagation in Fluids: Models and Numerical Techniques

The Fascinating World of Wave Propagation

The study of wave propagation in fluids is a captivating field that unveils the intricate behavior of waves as they travel through different media. Waves play a fundamental role in various natural phenomena, including ocean waves, seismic waves, and sound waves. Understanding how waves propagate in fluids is crucial for a wide range of applications such as earthquake prediction, sonar systems, and fluid dynamics simulations.

Models: Decoding Wave Propagation

To gain insights into wave propagation in fluids, scientists and engineers have developed various mathematical models that describe the behavior of waves. These models are based on fundamental physical principles and equations, enabling researchers to simulate and predict wave phenomena accurately. Two widely used models for wave propagation in fluids are the Linear Acoustics Model and the Navier-Stokes Equations Model.

1. Linear Acoustics Model

The Linear Acoustics Model is a simplified representation of wave propagation in compressible fluids. It assumes that the fluid is inviscid (no internal friction) and that the wave amplitudes are small. By employing linearizations of the governing equations, such as the Euler equations, this model provides a good approximation for high-frequency acoustic waves. It is commonly used in applications like ultrasonic imaging and underwater acoustics.

Wave Propagation in Fluids: Models and Numerical Techniques

by Vincent Guinot(2nd Edition, Kindle Edition)

5 out of 5

Language	:	English
File size	:	15302 KB
Text-to-Speech	:	Enabled
Screen Reader	:	Supported
Enhanced typesetting	:	Enabled
Word Wise	:	Enabled
Print length	:	674 pages
Lending	:	Enabled

FREE

2. Navier-Stokes Equations Model

The Navier-Stokes Equations Model is a more complex approach that considers the full dynamics of fluid flow, including the effects of viscosity and turbulence. By solving the Navier-Stokes equations numerically using advanced techniques like computational fluid dynamics (CFD),researchers can accurately capture the behavior of various types of waves, including water waves and atmospheric waves. This model is crucial for understanding tidal waves, weather patterns, and aerodynamics.

Numerical Techniques: Simulating Wave Propagation

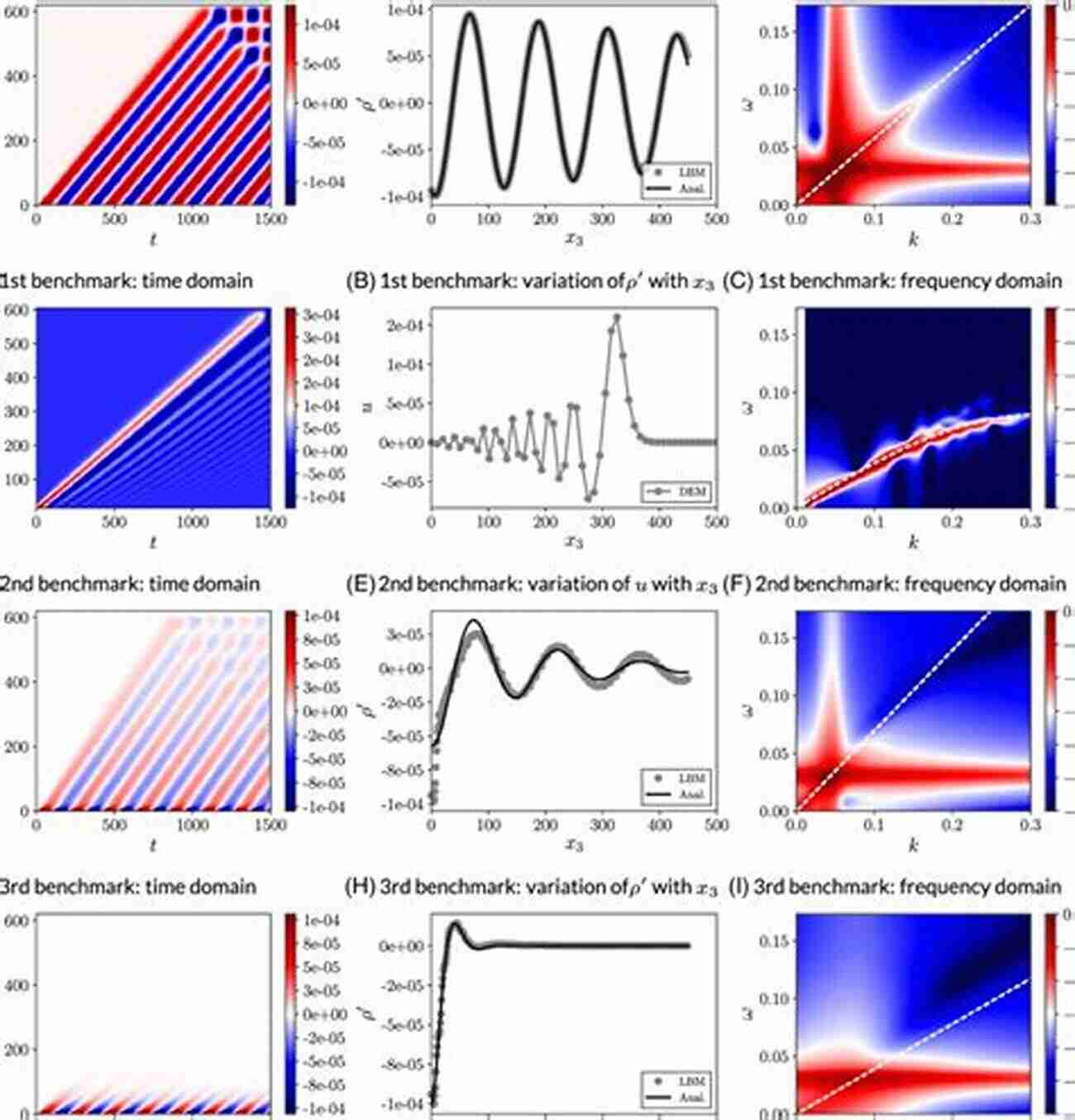
Solving the mathematical models of wave propagation in fluids requires sophisticated numerical techniques. Researchers have developed several numerical methods to accurately simulate and predict the complex behavior of waves. Some notable techniques include Finite Difference Methods (FDM),Finite Element Methods (FEM),and Finite Volume Methods (FVM). These methods discretize the governing equations and solve them iteratively on a computational grid, allowing for efficient computation of wave propagation.

1. Finite Difference Methods (FDM)

Finite Difference Methods approximate the derivatives in the governing equations by constructing a numerical grid and using finite differences to represent the derivatives. This technique is straightforward to implement and is widely used in wave propagation problems. However, it may struggle to handle irregular geometries and complex physical phenomena.

2. Finite Element Methods (FEM)

Finite Element Methods discretize the computational domain into smaller elements, where piecewise polynomial approximations are used to represent the solution. FEM excels at handling irregular geometries and capturing localized phenomena. It is often employed in structural analysis and fluid flow simulations.

3. Finite Volume Methods (FVM)

Finite Volume Methods divide the computational domain into control volumes and then integrate the governing equations over each volume. This approach conserves mass, momentum, and energy, making it suitable for problems involving mass or energy transport. FVM is commonly used in fluid dynamics simulations and combustion analysis.

: Unveiling the Secrets of Wave Propagation

Wave propagation in fluids is a captivating field that continues to astound scientists and researchers. Through the use of mathematical models and advanced numerical techniques, we can explore the intricate behaviors of waves in various media. These studies not only contribute to our fundamental understanding of natural phenomena but also pave the way for practical applications in multiple fields. By unraveling the mysteries of wave propagation, we unlock new opportunities to harness the power of waves for the betterment of our society.

Wave Propagation in Fluids: Models and Numerical Techniques

by Vincent Guinot(2nd Edition, Kindle Edition)

5 out of 5

Language	:	English
File size	:	15302 KB
Text-to-Speech	:	Enabled
Screen Reader	:	Supported
Enhanced typesetting	:	Enabled
Word Wise	:	Enabled
Print length	:	674 pages
Lending	:	Enabled

FREE

This second edition with four additional chapters presents the physical principles and solution techniques for transient propagation in fluid mechanics and hydraulics. The application domains vary including contaminant transport with or without sorption, the motion of immiscible hydrocarbons in aquifers, pipe transients, open channel and shallow water flow, and compressible gas dynamics.

The mathematical formulation is covered from the angle of conservation laws, with an emphasis on multidimensional problems and discontinuous flows, such as steep fronts and shock waves.

Finite difference-, finite volume- and finite element-based numerical methods (including discontinuous Galerkin techniques) are covered and applied to various physical fields. Additional chapters include the treatment of geometric source terms, as well as direct and adjoint sensitivity modeling for hyperbolic conservation laws. A concluding chapter is devoted to practical recommendations to the modeler.
Application exercises with on-line solutions are proposed at the end of the chapters.