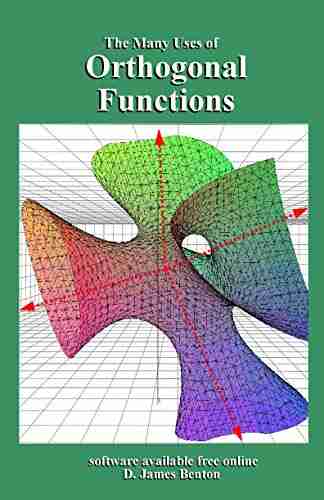
Orthogonal Functions: The Many Uses Of

Orthogonal functions play a fundamental role in various fields of mathematics, engineering, and physics. They provide a powerful tool for solving a wide range of problems and have found numerous applications in diverse areas. In this article, we will explore the concept of orthogonal functions, their properties, and some of their many practical uses.

Understanding Orthogonal Functions

Orthogonal functions are mathematical functions that are orthogonal to each other over a specific interval. In simpler terms, this means that when two different orthogonal functions are multiplied together and integrated over the interval, the resulting value is zero. This property makes them incredibly useful for solving differential equations and for approximating complex functions.

Orthogonal functions come in various forms, such as polynomials, trigonometric functions, and exponential functions. Each type of orthogonal function has its unique properties and applications.

Orthogonal Functions: The Many Uses of

by D. James Benton(Kindle Edition)

4.3 out of 5

Language	:	English
File size	:	7698 KB
Text-to-Speech	:	Enabled
Screen Reader	:	Supported
Enhanced typesetting	:	Enabled
Print length	:	113 pages
Lending	:	Enabled

FREE

Legendre Polynomials

Legendre polynomials are a type of orthogonal function that arises from solving the Legendre differential equation. These polynomials have found extensive use in physics and engineering, particularly in problems involving spherical symmetry and potential theory. They are also used in numerical methods to approximate functions and solve differential equations.

Fourier Series

The Fourier series is a representation of a function as an infinite sum of sinusoidal functions. The sinusoidal functions used in the Fourier series are orthogonal to each other over a specific interval, allowing us to accurately approximate a wide range of periodic functions. Fourier series has applications in signal processing, image compression, and solving partial differential equations.

Hermite Polynomials

Hermite polynomials are orthogonal functions that arise from solving the Hermite differential equation. These polynomials find applications in quantum mechanics, particularly in the study of the harmonic oscillator and quantum harmonic oscillators. They also play a crucial role in statistics and probability theory, where they are used to describe the probability distribution of certain random variables.

The Many Uses of Orthogonal Functions

Signal Processing

Orthogonal functions, such as the Fourier series, have revolutionized the field of signal processing. By decomposing a signal into its Fourier coefficients, we can analyze its frequency content, remove noise, and compress the data. This has led to advancements in fields such as telecommunications, audio and video processing, and image recognition.

Image Compression

Orthogonal functions, like the discrete cosine transform (DCT),are widely used in image compression algorithms. The DCT transforms the image into a set of frequency coefficients, which can be efficiently encoded and transmitted. This allows for significant reduction in file size without noticeable loss of image quality. Techniques like JPEG and MPEG are based on this principle.

Quantum Mechanics

Orthogonal functions play a crucial role in quantum mechanics, where wave functions representing physical systems are often expressed as linear combinations of orthogonal functions. This allows us to determine the probabilities of different outcomes when measuring observables. Orthogonal functions, such as the Hermite polynomials, facilitate the calculation of energy levels and transition probabilities in quantum systems.

Numerical Methods

Orthogonal functions are widely used in numerical methods for solving differential equations and approximating complex functions. By expanding a function in terms of orthogonal basis functions, we can represent it as a finite sum and solve the problem numerically. This approach provides accurate solutions while reducing computational complexity.

Statistics and Probability Theory

Orthogonal functions, like the Hermite polynomials, are used in statistics and probability theory to describe the probability distribution of certain random variables. By expressing the probability density function of a random variable as a series of orthogonal functions, we can analyze its properties, calculate moments, and estimate probabilities of events.

Orthogonal functions are a powerful mathematical tool with a wide range of applications. They have proven to be invaluable in solving differential equations, approximating complex functions, and understanding various physical phenomena. From signal processing to image compression, quantum mechanics to numerical methods, and statistics to probability theory, orthogonal functions play a vital role in advancing scientific knowledge and technological innovations. Exploring their properties and applications can deepen our understanding of the fundamental concepts of mathematics and their practical relevance.

Orthogonal Functions: The Many Uses of

by D. James Benton(Kindle Edition)

4.3 out of 5

Language	:	English
File size	:	7698 KB
Text-to-Speech	:	Enabled
Screen Reader	:	Supported
Enhanced typesetting	:	Enabled
Print length	:	113 pages
Lending	:	Enabled

FREE

Orthogonal functions are clever tools that unlock many mathematical puzzles. Once you've seen this done and understand how they work, you will find many more useful applications. This remarkable area of applied mathematics supports a wide range of technologies, ranging from CAT scans to satellite pictures from space to unraveling the sounds of the deep. Join me on a tour of this fascinating topic in which we will explore data sampling and approximation in both temporal and spatial dimensions.