Unlock the Power of Optimization Techniques in Statistics: Enhancing Statistical Modeling and Decision Science

Statistics, a branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data, plays a crucial role in various fields. It enables researchers and organizations to draw meaningful insights and make informed decisions. However, the real power of statistics lies in its optimization techniques, which can revolutionize statistical modeling and decision science.

What are Optimization Techniques?

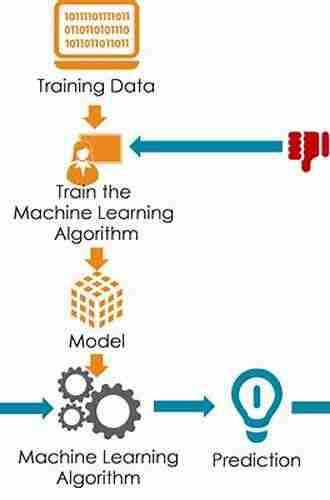
Optimization techniques refer to a set of mathematical methods used to find the best solutions for complex problems. In statistics, these techniques help in maximizing or minimizing an objective function while satisfying certain constraints. They aim to improve efficiency, accuracy, and decision-making by optimizing various statistical models.

Optimization techniques in statistics can be broadly classified into two categories: deterministic and stochastic. Deterministic optimization involves finding the optimal solution using mathematical equations and algorithms. On the other hand, stochastic optimization utilizes probabilistic models and algorithms to find near-optimal solutions in situations where randomness is involved.

Optimization Techniques in Statistics (Statistical Modeling and Decision Science)

by Jagdish S. Rustagi(Kindle Edition)

5 out of 5

Language	:	English
File size	:	25772 KB
X-Ray for textbooks	:	Enabled
Print length	:	359 pages
Screen Reader	:	Supported

FREE

The Role of Optimization Techniques in Statistical Modeling

Statistical modeling involves developing mathematical equations and models to describe and predict the relationships between variables. Optimization techniques can significantly enhance the accuracy and efficiency of statistical models, leading to more precise predictions and interpretations.

Some commonly used optimization techniques in statistical modeling include:

• Linear Programming: Linear programming helps in optimizing linear equations subject to linear constraints. It finds applications in resource allocation, production planning, portfolio optimization, and transportation.
• Nonlinear Programming: Nonlinear programming deals with optimizing nonlinear equations. It is used to solve complex optimization problems in various fields, such as economics, engineering, and data analysis.
• Integer Programming: Integer programming involves finding optimal solutions to linear or nonlinear equations with integer variables. It is useful in decision-making processes that involve discrete choices, such as project selection, scheduling, and facility location.
• Convex Programming: Convex programming deals with optimizing convex objective functions and convex constraints. It finds applications in machine learning, data fitting, signal processing, and image reconstruction.
• Dynamic Programming: Dynamic programming breaks complex problems into smaller subproblems, solving them iteratively. It is particularly useful in decision-making problems involving sequential actions and uncertain environments.

Optimization Techniques in Decision Science

Decision science involves making informed decisions based on available data, statistical models, and analyses. Optimization techniques play a crucial role in decision science by providing tools to optimize decision-making processes and improve outcomes.

Some optimization techniques used in decision science include:

• Game Theory: Game theory employs mathematical models to analyze and optimize decision-making in competitive situations. It helps in determining optimal strategies for players, maximizing overall outcomes, and predicting behavior.
• Queueing Theory: Queueing theory involves analyzing and optimizing waiting lines or queues. It finds applications in service industries, transportation, telecommunication networks, and healthcare systems.
• Network Optimization: Network optimization focuses on finding the most efficient paths or flows in networks. It is used in logistics, transportation planning, telecommunication routing, and supply chain management.
• Simulation Optimization: Simulation optimization combines simulation modeling with optimization techniques to find the best solution for complex systems. It is used in risk analysis, investment planning, and process improvement.

The Advantages of Optimization Techniques in Statistics and Decision Making

Optimization techniques offer numerous benefits in both statistical modeling and decision science:

• Improved Efficiency: By finding optimal solutions, optimization techniques enhance the efficiency of statistical models and decision-making processes. This leads to resource utilization, time management, and cost optimization.
• Enhanced Accuracy: Optimization techniques allow statisticians and decision-makers to make more accurate predictions and draw precise s. This, in turn, helps in minimizing errors and uncertainty.
• Robust Decision-Making: Optimization techniques enable the evaluation of multiple scenarios, trade-offs, and constraints to ensure robust decision-making. They provide insights into the potential outcomes of different options and help in selecting the most optimal course of action.
• Real-Time Decision Support: Using optimization techniques, decisions can be made in real-time, taking into account changing circumstances, constraints, and objectives. This enables organizations to respond quickly to dynamic environments.
• Competitive Advantage: Implementing optimization techniques gives organizations a competitive edge by streamlining processes, improving efficiency, and making better-informed decisions. This can lead to higher profitability, growth, and customer satisfaction.

Optimization techniques in statistics have the potential to revolutionize statistical modeling and decision science. They offer a wide range of methods to optimize objective functions, improve efficiency, and enhance decision-making processes. By embracing these techniques, researchers and organizations can unlock the power of data, making better-informed decisions and gaining a competitive advantage.

Optimization Techniques in Statistics (Statistical Modeling and Decision Science)

by Jagdish S. Rustagi(Kindle Edition)

5 out of 5

Language	:	English
File size	:	25772 KB
X-Ray for textbooks	:	Enabled
Print length	:	359 pages
Screen Reader	:	Supported

FREE

Statistics help guide us to optimal decisions under uncertainty. A large variety of statistical problems are essentially solutions to optimization problems. The mathematical techniques of optimization are fundamentalto statistical theory and practice. In this book, Jagdish Rustagi provides full-spectrum coverage of these methods, ranging from classical optimization and Lagrange multipliers, to numerical techniques using gradients or direct search, to linear, nonlinear, and dynamic programming using the Kuhn-Tucker conditions or the Pontryagin maximal principle. Variational methods and optimization in function spaces are also discussed, as are stochastic optimization in simulation, including annealing methods.

The text features numerous applications, including: Finding maximum likelihood estimates, Markov decision processes, Programming methods used to optimize monitoring of patients in hospitals, Derivation of the Neyman-Pearson lemma, The search for optimal designs, Simulation of a steel mill.

Suitable as both a reference and a text, this book will be of interest to advanced undergraduate or beginning graduate students in statistics, operations research, management and engineering sciences, and related fields. Most of the material can be covered in one semester by students with a basic background in probability and statistics.

• Covers optimization from traditional methods to recent developments such as Karmarkars algorithm and simulated annealing
• Develops a wide range of statistical techniques in the unified context of optimization
• Discusses applications such as optimizing monitoring of patients and simulating steel mill operations
• Treats numerical methods and applications
• Includes exercises and references for each chapter
• Covers topics such as linear, nonlinear, and dynamic programming, variational methods, and stochastic optimization