Unlocking the Secrets of Trigonometric Functions: An Ellipse Cheat Sheet for the First Quadrant

Trigonometric functions play a fundamental role in mathematics, allowing us to understand the relationships between angles and sides of geometric figures. While most of us are familiar with trigonometry in the context of triangles, there is another fascinating application of trigonometric functions – the ellipse. In this article, we will delve into the world of ellipses and provide you with an invaluable cheat sheet for understanding the trigonometric functions specific to the first quadrant of an ellipse.

What is an Ellipse?

An ellipse is a closed curve that is shaped like a flattened circle. It is defined as the set of all points in a plane, such that the sum of the distances between each point and two fixed points (called foci) is constant. The major axis of the ellipse is the longest segment that passes through the center and ends at two points on the curve, while the minor axis is the perpendicular segment that passes through the center.

The first quadrant of an ellipse is the portion of the curve that lies above the x-axis and to the right of the y-axis. Understanding the trigonometric functions specific to this quadrant is crucial for solving problems related to ellipses.

Ellipsometry: Trigonometric Functions of an Ellipse - Cheat Sheet for the First Quadrant

by American Math Academy(Kindle Edition)

4.3 out of 5

Language	:	English
File size	:	3150 KB
Text-to-Speech	:	Enabled
Enhanced typesetting	:	Enabled
Print length	:	17 pages
Screen Reader	:	Supported
Hardcover	:	544 pages
Item Weight	:	2.09 pounds
Dimensions	:	6 x 1.19 x 9 inches

FREE

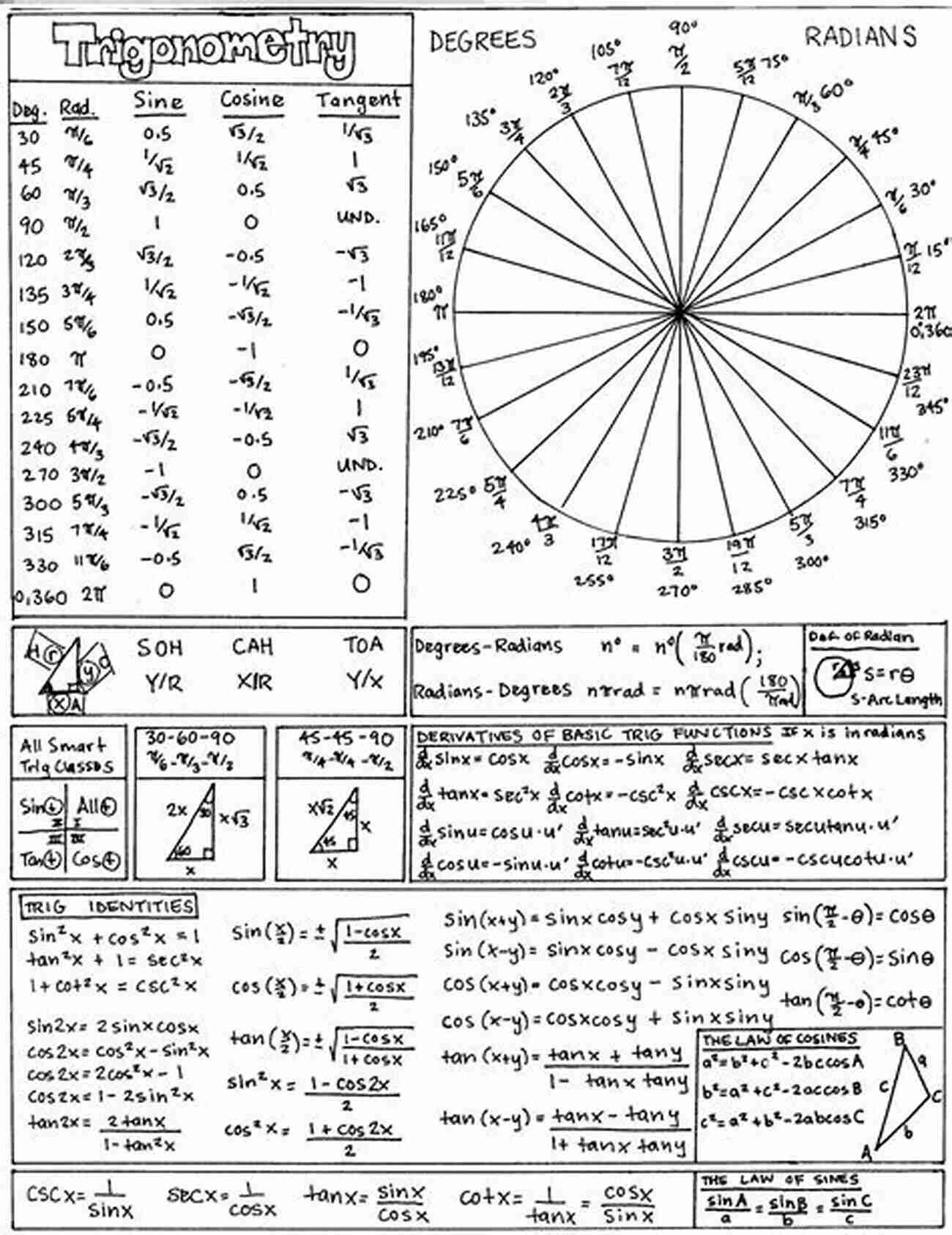
The Trigonometric Functions of an Ellipse Cheat Sheet

In the context of an ellipse in the first quadrant, the trigonometric functions are as follows:

1. Sine (sin)

The sine function relates the ratio of the length of the y-coordinate of a point on the ellipse to the length of the semi-major axis. In the first quadrant, the sine function varies between 0 and 1, with a maximum value of 1 when the angle is 90 degrees (π/2 radians).

Formula: sin(θ) = y / a

2. Cosine (cos)

The cosine function relates the ratio of the length of the x-coordinate of a point on the ellipse to the length of the semi-major axis. In the first quadrant, the cosine function also varies between 0 and 1, with a maximum value of 1 when the angle is 0 degrees (0 radians).

Formula: cos(θ) = x / a

3. Tangent (tan)

The tangent function relates the ratio of the length of the y-coordinate of a point on the ellipse to the length of the x-coordinate. In the first quadrant, the tangent function varies between 0 and infinity. It is worth noting that the tangent function can also be expressed as the sine function divided by the cosine function.

Formula: tan(θ) = (y / a) / (x / a) = y / x

4. Secant (sec)

The secant function relates the ratio of the length of the semi-major axis to the length of the x-coordinate of a point on the ellipse. In the first quadrant, the secant function also varies between 1 and infinity. It is worth noting that the secant function is the reciprocal of the cosine function.

Formula: sec(θ) = a / x

5. Cosecant (csc)

The cosecant function relates the ratio of the length of the semi-major axis to the length of the y-coordinate of a point on the ellipse. In the first quadrant, the cosecant function also varies between 1 and infinity. It is worth noting that the cosecant function is the reciprocal of the sine function.

Formula: csc(θ) = a / y

6. Cotangent (cot)

The cotangent function relates the ratio of the length of the x-coordinate of a point on the ellipse to the length of the y-coordinate. In the first quadrant, the cotangent function also varies between 0 and infinity. It is worth noting that the cotangent function is the reciprocal of the tangent function.

Formula: cot(θ) = (x / a) / (y / a) = x / y

By understanding these trigonometric functions specific to the first quadrant of an ellipse, you can unlock the ability to analyze and solve complex problems involving ellipses.

Trigonometry is a powerful tool that extends beyond triangles, with applications in various geometric shapes, including ellipses. Understanding the trigonometric functions specific to the first quadrant of an ellipse empowers you to solve problems related to this fascinating curve. With the cheat sheet provided in this article, you can explore the secrets of trigonometric functions and master the art of working with ellipses.

Ellipsometry: Trigonometric Functions of an Ellipse - Cheat Sheet for the First Quadrant

by American Math Academy(Kindle Edition)

4.3 out of 5

Language	:	English
File size	:	3150 KB
Text-to-Speech	:	Enabled
Enhanced typesetting	:	Enabled
Print length	:	17 pages
Screen Reader	:	Supported
Hardcover	:	544 pages
Item Weight	:	2.09 pounds
Dimensions	:	6 x 1.19 x 9 inches

FREE

In the study of triangles and trigonometry, we consider the unit circle which, by definition is an ellipse of eccentricity zero. What happens to the trigonometric functions when the eccentricity is different from zero? This short booklet provides an extracted cheat sheet version of the answer to this question.
Trigonometric functions, including the calculation of the arc length of an ellipse are presented for ellipses for any generic ellipse or a specific ellipse called the Unit Ellipse having its' minor-semi axis equal to [a=1] and its major-semi axis [sqrt 2], calculated for any given angle, between 0°-90°, for the radius being a function of the given angle.
This short booklet is the version to the subject matter until the release of the complete book with theory and proof.